标准差公式是什么？

在数据分析与统计学领域，标准差是一个极为重要的概念，它为我们提供了一种量化数据离散程度的手段。标准差公式作为计算这一指标的核心工具，在日常的数据处理、科学实验、金融分析等多个领域都有着广泛的应用。本文将从标准差的基本概念、计算公式的推导、公式的实际应用以及标准差公式的局限性等多个维度，对标准差公式进行深入探讨。

一、标准差的基本概念

标准差（Standard Deviation），通常记为σ（sigma），是统计学中用于描述数据分布离散程度的一个关键指标。与方差（Variance）不同，标准差具有与原始数据相同的单位，因此更便于直观理解和比较。标准差越小，表示数据点越接近平均值，即数据的分布越集中；标准差越大，表示数据点越分散，数据的分布越广泛。

二、标准差公式的推导

标准差的计算基于方差，因此首先需要了解方差的定义和计算公式。方差是每个数据点与平均值之差的平方的平均值，其公式为：

\[ \text{方差} = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2 \]

其中，\(N\) 是数据点的数量，\(x_i\) 是每个数据点的值，\(\mu\) 是数据的平均值。

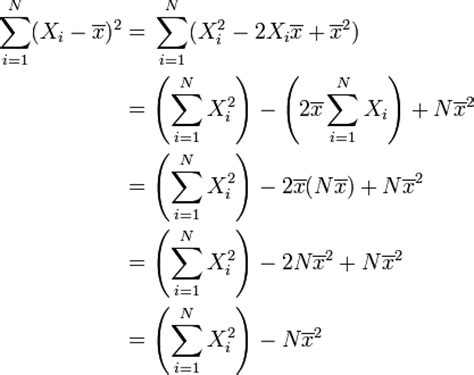
标准差的计算公式则是方差的平方根，即：

\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \]

这里的 \(\sigma\) 就是标准差。

为了处理样本数据（而非整个数据集）时可能引入的偏差，通常还会使用修正后的标准差公式，即样本标准差公式：

\[ s = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} (x_i - \bar{x})^2} \]

其中，\(s\) 是样本标准差，\(N-1\) 是自由度（因为样本均值的使用减少了一个自由度），\(\bar{x}\) 是样本均值。

三、标准差公式的实际应用

标准差公式在多个领域都有着广泛的应用，以下是一些具体的例子：

1. 金融分析：在金融领域，标准差常用于衡量投资组合的风险。一个投资组合的标准差越大，说明其价格波动越剧烈，风险越高；反之，标准差越小，说明其价格波动越平稳，风险越低。

2. 质量控制：在制造业中，标准差用于评估生产过程的稳定性和一致性。通过监控产品的标准差，制造商可以及时发现生产过程中的异常波动，从而采取相应措施提高产品质量。

3. 科学研究：在科学实验中，标准差用于量化实验结果的离散程度。一个实验结果的标准差越小，说明实验数据的重复性越好，实验结果越可靠；反之，标准差越大，说明实验数据的离散性越大，实验结果的可信度越低。

4. 教育评估：在教育领域，标准差可以用于评估考试成绩的分布情况。一个班级考试成绩的标准差越小，说明学生的成绩越集中，教学效果越均衡；反之，标准差越大，说明学生的成绩差异越大，教学效果可能存在不均衡的问题。

5. 市场分析：在市场分析中，标准差可以用于评估消费者需求的分布情况。一个产品的需求标准差越小，说明消费者的需求越集中，市场定位越明确；反之，标准差越大，说明消费者的需求差异越大，市场定位可能更加模糊。

四、标准差公式的局限性

尽管标准差公式在多个领域都有着广泛的应用，但它也存在一些局限性：

1. 对异常值的敏感性：标准差对异常值（极端值）非常敏感。一个或少数几个异常值可能会导致整个数据集的标准差显著增大，从而影响对数据分布离散程度的准确评估。

2. 对分布形状的假设：标准差公式基于数据的方差进行计算，而方差假设数据分布是对称的。然而，在实际应用中，数据分布往往不是完全对称的。因此，在数据分布不对称的情况下，标准差可能无法准确反映数据的离散程度。

3. 缺乏方向性信息：标准差只能量化数据的离散程度，而无法提供数据分布的方向性信息。例如，两个数据集可能有相同的标准差，但它们的分布方向可能完全不同。

4. 对量纲的依赖：标准差具有与原始数据相同的单位，这虽然便于直观理解，但也使得标准差在不同量纲的数据之间难以直接比较。

5. 样本大小的影响：当样本量较小时，样本标准差可能会受到样本随机性的影响而波动较大。随着样本量的增加，样本标准差的稳定性会逐渐提高。

为了克服这些局限性，统计学家和数据分析师在实际应用中通常会结合其他统计指标和图形工具（如箱线图、直方图等）来全面评估数据的分布情况。

五、结论

标准差公式作为量化数据离散程度的重要工具，在数据分析与统计学领域发挥着不可替代的作用。通过计算标准差，我们可以深入了解数据的分布情况，为决策提供有力支持。然而，标准差公式也存在一定的局限性，需要在实际应用中