如何判断函数的奇偶性才是最好的方法？

在数学中，函数的奇偶性是一个重要而基础的概念。它不仅帮助我们理解函数的性质，还能简化很多计算和分析过程。本文将详细介绍判断函数奇偶性的几种方法，并探讨其中的“最好”方法。通过理解这些方法的适用条件和优缺点，读者可以更加全面地掌握这一知识点。

一、奇偶性的定义

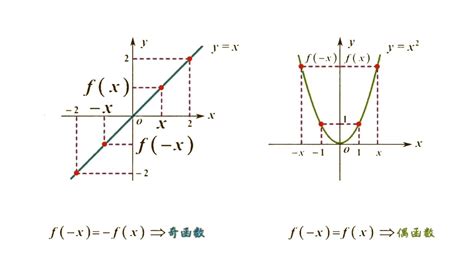
首先，我们需要明确函数奇偶性的定义。设函数f(x)的定义域为D，如果对于D内的任意x，都有f(-x)=-f(x)，则称f(x)为奇函数；如果对于D内的任意x，都有f(-x)=f(x)，则称f(x)为偶函数。如果函数既不满足奇函数的定义，也不满足偶函数的定义，则称该函数为非奇非偶函数。

二、常见的判断方法

1. 代数法

代数法是最直观的判断方法。对于给定的函数f(x)，我们直接计算f(-x)，然后比较f(-x)与f(x)的关系。

如果f(-x)=-f(x)，则f(x)是奇函数。

如果f(-x)=f(x)，则f(x)是偶函数。

例1：判断函数f(x)=x^3-x的奇偶性。

计算f(-x)：f(-x)=(-x)^3-(-x)=-x^3+x=-(x^3-x)=-f(x)。

因此，f(x)=x^3-x是奇函数。

例2：判断函数f(x)=x^2+1的奇偶性。

计算f(-x)：f(-x)=(-x)^2+1=x^2+1=f(x)。

因此，f(x)=x^2+1是偶函数。

2. 图像法

图像法是通过观察函数的图像来判断其奇偶性。

如果函数图像关于原点对称，则函数是奇函数。

如果函数图像关于y轴对称，则函数是偶函数。

这种方法直观易懂，但前提是能够准确地画出函数的图像。对于一些复杂函数，图像可能难以绘制或观察。

例3：判断函数f(x)=sin(x)的奇偶性。

观察sin(x)的图像，我们发现它关于原点对称。因此，f(x)=sin(x)是奇函数。

例4：判断函数f(x)=cos(x)的奇偶性。

观察cos(x)的图像，我们发现它关于y轴对称。因此，f(x)=cos(x)是偶函数。

3. 定义域法

定义域法是通过分析函数的定义域来判断其奇偶性。

如果函数的定义域不关于原点对称，则函数既不是奇函数也不是偶函数。

如果函数的定义域关于原点对称，但f(-x)与f(x)没有确定的关系，则函数也是非奇非偶函数。

这种方法快速有效，但只能排除一些显然非奇非偶的情况，不能给出函数是奇函数还是偶函数的明确答案。

例5：判断函数f(x)=1/x的奇偶性。

函数f(x)=1/x的定义域为{x|x≠0}，这个定义域关于原点对称。计算f(-x)：f(-x)=-1/x=-f(x)。因此，f(x)=1/x是奇函数。

例6：判断函数f(x)=√x的奇偶性。

函数f(x)=√x的定义域为[0,+∞)，这个定义域不关于原点对称。因此，f(x)=√x是非奇非偶函数。

4. 性质法

性质法是利用函数的已知性质来判断其奇偶性。例如，如果知道函数是周期函数，可以结合周期性和奇偶性的关系来判断。这种方法适用于一些特殊类型的函数，如三角函数、指数函数等。

例7：判断函数f(x)=e^x的奇偶性。

函数f(x)=e^x是指数函数，其图像既不关于原点对称也不关于y轴对称。计算f(-x)：f(-x)=e^(-x)=1/e^x≠e^x且≠-e^x。因此，f(x)=e^x是非奇非偶函数。

例8：判断函数f(x)=tan(x)的奇偶性。

函数f(x)=tan(x)是正切函数，其