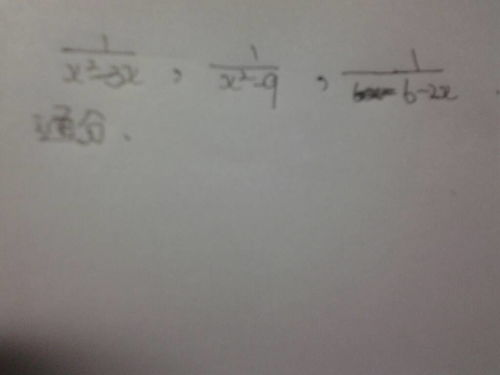
在数学的浩瀚宇宙中,分数运算无疑是许多同学心中的“小恶魔”。无论是加法、减法、乘法还是除法,分数运算总离不开一个关键步骤——找公分母。而最简公分母,更是让不少同学头疼不已。别担心,今天我们就来一场“最简公分母大揭秘”,让你轻松掌握这个数学小技巧,从此分数运算不再头疼!

首先,我们要明白什么是公分母,以及为什么要找最简公分母。

公分母:两个或多个分数进行加减运算时,为了统一分数单位,需要找到一个公共的分母,这个公共的分母就是公分母。
最简公分母:在所有的公分母中,最小且不能再简化的那个,就是最简公分母。
为什么要找最简公分母呢?很简单,最简公分母能确保我们在进行分数运算时,既不会遗漏任何可能的简化步骤,也不会因为分母过于复杂而增加计算难度。
找公分母,其实就像是在寻找两个或多个分数的“最小公倍数”的升级版。下面,我们就来一步步学习如何找到公分母。
首先,我们需要将每个分数的分母进行质因数分解。质因数分解就是把一个数分解成若干个质数相乘的形式。
例如,对于分数1/6和1/9,我们可以将它们的分母6和9进行质因数分解:
6 = 2 × 3
9 = 3 × 3
接下来,我们需要找出所有出现的质因数,以及它们出现的最高次数。
在上面的例子中,质因数有2和3。其中,2出现了1次,3出现了2次(因为9中有两个3)。
最后,我们将所有质因数按照它们出现的最高次数相乘,得到的就是最简公分母。
所以,对于分数1/6和1/9,它们的最简公分母就是:
2 × 3 × 3 = 18
掌握了基本步骤后,我们再来看看如何应对一些更复杂的情况。
当分数的分母含有字母时,我们同样可以进行质因数分解,但需要注意字母的指数。
例如,对于分数1/(2a)和1/(3a^2),我们可以将它们的分母进行质因数分解(这里把字母也看作是一种“因数”):
2a = 2 × a^1
3a^2 = 3 × a^2
然后,找出所有质因数(包括字母)以及它们出现的最高次数:
质因数有2、3和a,其中2和3各出现了1次,a出现了2次。
所以,它们的最简公分母就是:
2 × 3 × a^2 = 6a^2
当有多个分数需要找最简公分母时,我们只需要按照上面的步骤,对每个分数的分母进行质因数分解,然后找出所有质因数以及它们出现的最高次数,最后相乘即可。
例如,对于分数1/6、1/9和1/12,我们可以将它们的分母进行质因数分解:
6 = 2 × 3
9 = 3 × 3
12 = 2 × 2 × 3
然后,找出所有质因数以及它们出现的最高次数:
质因数有2和3,其中2出现了2次(因为12中有两个2),3出现了2次。
所以,它们的最简公分母就是:
2 × 2 × 3 × 3 = 36
说了这么多,不如来几道例题练练手吧!
例题1:找出分数1/8和3/12的最简公分母。
解答:
1. 分解质因数:
8 = 2 × 2 × 2
12 = 2 × 2 × 3
2. 找出所有质因数以及它们出现的最高次数:
质因数有2和3,其中2出现了3次,3出现了1次。
3. 构建最简公分母:
2 × 2 × 2 × 3 = 24
所以,分数1/8和3/12的最简公分母是24。
例题2:找出分数2/(3x)和1/(4x^2y)的最简公分母。
解答:
1. 分解质因数(包括字母):
3x = 3 × x^1
4x^2y = 2 × 2 × x^2 × y^1
2. 找出所有质因数(包括字母)以及它们出现的最高次数:
质因数有2、3、x和y,其中2出现了2次,3出现了1次,x出现了2次,y出现了1次。
3. 构建最简公分母:
2 × 2 × 3 × x^2 × y = 12x^2y
所以,分数2/(3x)和1/(4x^2y)的最简公分母是12x^2y。
通过上面的学习,相信你已经掌握了如何找到最简公分母的方法。记住,无论是基础篇还是进阶篇的技巧,都是为了让我们在进行分数运算时更加得心应手。
最简公分母不仅是一个数学工具,更是一种思维方式。它教会我们如何化繁为简,如何在复杂的数学世界中找到规律和方法。
所以,下次当你面对分数运算时,不要再感到头疼和害怕。试着用我们今天学到的方法,去找到那个最简公分母,你会发现,原来分数运算也可以变得简单有趣!
现在,你已经解锁了“最简公分母”这个数学小技巧,赶快去实践一下吧!相信你会在分数运算的世界里,找到属于自己的乐趣和成就感!
89.53M欧洲卡车模拟器3游戏
88.19M长风视频app免费版
85.65M酷安客户端v13.0.1去广告版
66.62M酷漫屋下拉式免费漫画
60.17M妙语星河app
72.04M冷颜框架3.0防闪版本
65.53M梵音瑜伽app
73.48M防御矩阵异形入侵
62.27MMadOut2 BCO
10.62M终身教育平台
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 琼ICP备2024021917号-12