三角形ABC中角平分线CD的性质探究

探索三角形角平分线的奥秘：当BC遇上AC，CD如何成为解题关键？

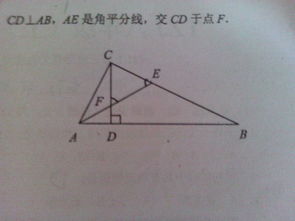
在数学的广阔天地里，三角形以其简洁而深邃的魅力，吸引着无数探索者的目光。今天，我们将一同走进一个关于三角形角平分线的奇妙世界，揭开它神秘的面纱。已知条件很简单：在三角形ABC中，CD是三角形ABC的角平分线。但正是这条看似不起眼的线，却蕴含着丰富的数学知识和解题技巧。

首先，让我们明确一下什么是三角形的角平分线。在一个三角形中，从一个角的顶点出发，将该角平分，并与对边相交，连接顶点和交点的线段就叫做这个三角形的角平分线。在我们的已知条件中，CD正是三角形ABC中角C的角平分线。

现在，让我们想象一下这个三角形ABC。它可能是一个锐角三角形、直角三角形，甚至是一个钝角三角形。无论它的形状如何，CD作为角C的角平分线，总是扮演着特殊的角色。它不仅是角C的平分线，更是连接三角形两边的重要桥梁。

接下来，我们来看看当BC遇上AC时，CD会如何发挥作用。在这里，“遇上”并不仅仅意味着两条线段相交，而是指它们与CD之间可能存在的某种关系或规律。为了更直观地理解这一点，我们可以考虑一些具体的数学问题。

问题一：求证三角形BCD与三角形ACD的面积之比等于BC与AC之比。

这是一个关于三角形面积比的问题。我们知道，三角形的面积与它的底和高有关。在这里，我们可以将BC和AC看作是两个三角形的底，而CD则可以看作是它们共同的高（因为CD是角C的角平分线，所以到两边的距离相等）。因此，根据三角形面积的计算公式，我们可以得出三角形BCD与三角形ACD的面积之比等于BC与AC之比。

这个问题不仅展示了CD作为角平分线的独特性质，还让我们深刻理解了三角形面积与底、高之间的关系。

问题二：在三角形ABC中，若角B的平分线与角C的平分线相交于点O，求证AO是角BAC的平分线。

这是一个关于三角形内角平分线交点的问题。在三角形中，三条内角平分线的交点叫做三角形的内心。根据三角形的性质，我们知道内心到三角形三边的距离是相等的。因此，如果我们能够证明AO到角BAC的两边AB和AC的距离相等，就可以证明AO是角BAC的平分线。

在这个问题中，CD作为角C的角平分线，为我们提供了一个重要的线索。我们可以利用CD的性质，结合其他已知条件，逐步推导出AO是角BAC的平分线的结论。

这个问题不仅考察了我们对三角形内角平分线交点的理解，还锻炼了我们的逻辑推理能力和空间想象能力。

除了以上两个问题外，CD作为三角形ABC的角平分线，还可以与其他知识点相结合，形成更多有趣且富有挑战性的数学问题。例如，我们可以考虑在三角形ABC中添加一个点P，使得PC垂直于CD，然后探讨点P与三角形ABC其他边或角的关系。

这样的问题不仅丰富了我们对三角形角平分线的认识，还让我们更加深入地理解了三角形与其他几何图形之间的内在联系。

当然，在解决这些问题的过程中，我们也需要掌握一些基本的数学方法和技巧。例如，利用三角形的全等或相似来证明线段或角的关系；利用三角形的面积公式来计算或比较不同三角形的面积；利用三角形的内角和性质来求解未知角等。

这些方法和技巧不仅能够帮助我们解决具体的问题，还能够提高我们的数学素养和解题能力。因此，在学习三角形角平分线的过程中，我们应该注重对这些方法和技巧的掌握和运用。

此外，我们还可以通过绘制图形、观察规律、动手操作等方式来加深对三角形角平分线的理解和认识。例如，我们可以使用几何画板等工具来绘制不同形状的三角形，并观察它们角平分线的位置和性质；我们可以尝试用纸片或塑料片等材料制作三角形模型，并亲手操作来感受角平分线的存在和作用。

这些实践活动不仅能够让我们更加直观地理解三角形角平分线的概念，还能够激发我们对数学学习的兴趣和热情。

总之，三角形角平分线是一个充满魅力和挑战的数学话题。通过学习和探索这个话题，我们可以更加深入地理解三角形的性质和规律，提高我们的数学素养和解题能力。同时，我们也可以从中感受到数学的魅力和乐趣，激发我们对数学学习的热情和动力。

在未来的学习和生活中，让我们继续保持对数学的热爱和探索精神，不断挖掘和发现数学世界中的奥秘和奇迹。相信在不久的将来，我们一定能够在数学的广阔天地中展翅高飞，创造属于自己的辉煌和成就！